Neocijenjeno
4. srpnja 2016. 15:34 (9 godine, 8 mjeseci)
Let

,

,

,

,

be points such that

is a cyclic quadrilateral and
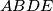
is a parallelogram. The diagonals

and

intersect at

and the rays

and
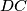
intersect at

. Prove that
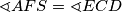
.
%V0
Let $A$, $B$, $C$, $D$, $E$ be points such that $ABCD$ is a cyclic quadrilateral and $ABDE$ is a parallelogram. The diagonals $AC$ and $BD$ intersect at $S$ and the rays $AB$ and $DC$ intersect at $F$. Prove that $\sphericalangle{AFS}=\sphericalangle{ECD}$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Neka su
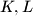
nožišta visina iz

na redom
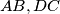
. Kako je
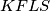
tetivan slijedi da je
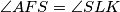
.
Kako je

tetivan vrijedi
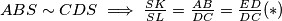
.
Primijetimo da je
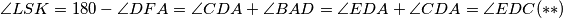
.
Iz

i
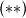
slijedi da je
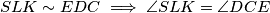
iz čega slijedi traženo.
%V0
Neka su $K,L$ nožišta visina iz $S$ na redom $AB,DC$. Kako je $KFLS$ tetivan slijedi da je $\angle AFS = \angle SLK$.
Kako je $ABCD$ tetivan vrijedi $ABS \sim CDS \implies \frac{SK}{SL}= \frac{AB}{DC}= \frac {ED}{DC} (*)$.
Primijetimo da je $\angle LSK = 180 - \angle DFA = \angle CDA + \angle BAD = \angle EDA + \angle CDA = \angle EDC (**)$.
Iz $(*)$ i $(**)$ slijedi da je $SLK \sim EDC \implies \angle SLK = \angle DCE$ iz čega slijedi traženo.