Točno
25. srpnja 2016. 23:22 (9 godine, 7 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Neka 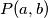 označava uvrštavanje brojeva
označava uvrštavanje brojeva  i
i  umjesto
umjesto  i
i  u početnu jednadžbu.
u početnu jednadžbu.
Neka je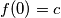 i
i 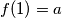

Promotrimo dva slučaja:
1.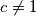
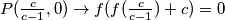
Neka je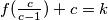 . (vrijedi
. (vrijedi 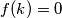 )
)
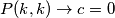 (sada lako vidimo
(sada lako vidimo 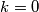 )
)

Pretpostavimo da postoji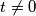 takav da je
takav da je 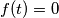 .
.
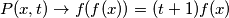
Iz ovoga i iz zaključujemo da mora biti
zaključujemo da mora biti 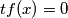 i imamo dva podslučaja:
i imamo dva podslučaja:
1.1.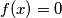 za svaki realan
za svaki realan  .
.
Provjerom (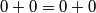 ) utvrđujemo da je jedno rješenje zadatka
) utvrđujemo da je jedno rješenje zadatka 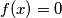 za svaki realan x.
za svaki realan x.
1.2.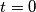
Ovo je kontradikcija i zaključujemo da je jedini realan koji zadovoljava
koji zadovoljava 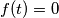 nula. Budući da imamo injektivnost u nuli sigurno postoji
nula. Budući da imamo injektivnost u nuli sigurno postoji 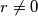 takav da je
takav da je 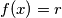 za neki
za neki  . Iz
. Iz  je
je 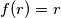 .
.
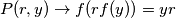 pa je
pa je  surjekcija.
surjekcija.
Sada u izrazu
u izrazu  može poprimiti vrijednost svakog realnog broja (postoji
može poprimiti vrijednost svakog realnog broja (postoji  koji zadovoljava
koji zadovoljava 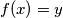 za svaki realan
za svaki realan  ) iz čega dobivamo rješenje
) iz čega dobivamo rješenje 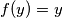 koje provjerimo:
koje provjerimo: 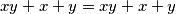
2.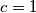
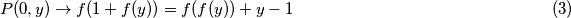
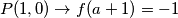
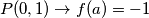
Iz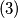 vidimo da
vidimo da  ovisi o
ovisi o 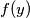 , odnosno
, odnosno  je injekcija, ali
je injekcija, ali 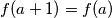 i time dobivamo kontradikciju za slučaj
i time dobivamo kontradikciju za slučaj 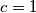
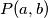 označava uvrštavanje brojeva
označava uvrštavanje brojeva  i
i  umjesto
umjesto  i
i  u početnu jednadžbu.
u početnu jednadžbu.Neka je
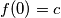 i
i 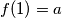

Promotrimo dva slučaja:
1.
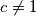
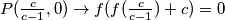
Neka je
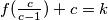 . (vrijedi
. (vrijedi 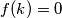 )
)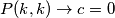 (sada lako vidimo
(sada lako vidimo 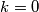 )
)
Pretpostavimo da postoji
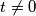 takav da je
takav da je 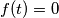 .
.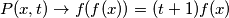
Iz ovoga i iz
 zaključujemo da mora biti
zaključujemo da mora biti 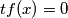 i imamo dva podslučaja:
i imamo dva podslučaja:1.1.
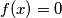 za svaki realan
za svaki realan  .
.Provjerom (
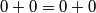 ) utvrđujemo da je jedno rješenje zadatka
) utvrđujemo da je jedno rješenje zadatka 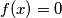 za svaki realan x.
za svaki realan x.1.2.
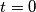
Ovo je kontradikcija i zaključujemo da je jedini realan
 koji zadovoljava
koji zadovoljava 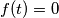 nula. Budući da imamo injektivnost u nuli sigurno postoji
nula. Budući da imamo injektivnost u nuli sigurno postoji 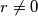 takav da je
takav da je 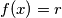 za neki
za neki  . Iz
. Iz  je
je 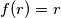 .
.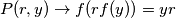 pa je
pa je  surjekcija.
surjekcija.Sada
 u izrazu
u izrazu  može poprimiti vrijednost svakog realnog broja (postoji
može poprimiti vrijednost svakog realnog broja (postoji  koji zadovoljava
koji zadovoljava 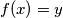 za svaki realan
za svaki realan  ) iz čega dobivamo rješenje
) iz čega dobivamo rješenje 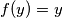 koje provjerimo:
koje provjerimo: 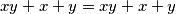
2.
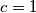
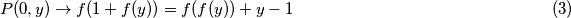
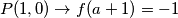
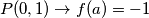
Iz
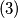 vidimo da
vidimo da  ovisi o
ovisi o 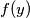 , odnosno
, odnosno  je injekcija, ali
je injekcija, ali 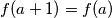 i time dobivamo kontradikciju za slučaj
i time dobivamo kontradikciju za slučaj 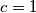
 Školjka
Školjka 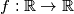 , such that
, such that 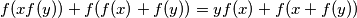 holds for all
holds for all 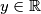 , where
, where 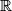 denotes the set of real numbers.
denotes the set of real numbers.