Točno
12. rujna 2016. 21:41 (9 godine, 4 mjeseci)
Dva prosta broja, $p,q(p>q)$ , zadovoljavaju $p^q + 9q^6 = k^2$ gdje je $k$ prirodan broj. Pronađi $p + q$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
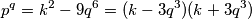
Prema tome, imamo za
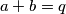
:
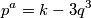
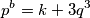
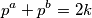
odakle ili
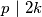
ili
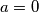
. Očito,
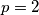
nije rješenje zbog

pa imamo
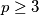
Nadalje, ako
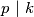
tada
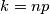
pa
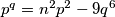
pa
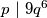
.
No, tada bi bilo ili
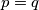
što nije moguće po uvjetu

ili
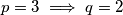
što nije rješenje (a time imamo i
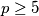
)
Zaključujemo da
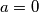
.
Tada:
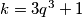
pa
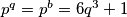
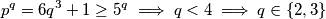
Ako
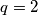
tada
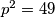
pa
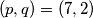
Ako
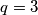
tada
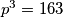
pa nema rješenja.
Prema tome
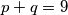
.
%V0
$$p^q = k^2 - 9q^6 = (k-3q^3)(k+3q^3)$$
Prema tome, imamo za $a+b=q$:
$$p^a = k - 3q^3$$
$$p^b = k + 3q^3$$
$$p^a + p^b = 2k$$
odakle ili $p \ | \ 2k$ ili $a = 0$. Očito, $p = 2$ nije rješenje zbog $p > q$ pa imamo $p \geq 3$
Nadalje, ako $p \ | \ k$ tada $k = np$ pa $p^q = n^2p^2 - 9q^6$ pa $p \ | \ 9q^6$.
No, tada bi bilo ili $p = q$ što nije moguće po uvjetu $ p > q$ ili $p=3 \implies q = 2$ što nije rješenje (a time imamo i $p \geq 5$)
Zaključujemo da $a =0$.
Tada: $k = 3q^3 + 1$ pa $p^q = p^b = 6q^3 + 1$
$$p^q = 6q^3+1 \geq 5^q \implies q < 4 \implies q \in \{2, 3\}$$
Ako $q = 2$ tada $p^2 = 49$ pa $(p, q) = (7, 2)$
Ako $q = 3$ tada $p^3 = 163$ pa nema rješenja.
Prema tome $p+q = 9$.