Točno
16. travnja 2012. 00:30 (13 godine, 10 mjeseci)
Dan je pravokutan trokut

s pravim kutom pri vrhu

, u kojem je

polovište katete

. Dokaži da je
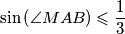
. Kada se postiže jednakost?
%V0
Dan je pravokutan trokut $ABC$ s pravim kutom pri vrhu $C$, u kojem je $M$ polovište katete $\overline{BC}$. Dokaži da je $\displaystyle \sin\left(\angle{MAB}\right) \leqslant \frac 13$. Kada se postiže jednakost?
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
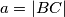
,
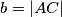
Neka je

nožište visine iz

na

.
Trokut
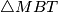
je sličan trokutu

pa vrijedi:
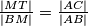
.
Iz ovog slijedi da je
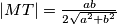
.
Također vrijedi
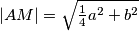
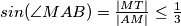
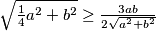
Kvadriranjem i sređivanjem dobijemo:
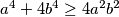
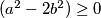
Jednakost vrijedi kada je
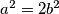
.
%V0
$a = |BC|$, $b = |AC|$ \
Neka je $T$ nožište visine iz $M$ na $\overline{AB}$.
Trokut $\triangle MBT$ je sličan trokutu $\triangle ABC$ pa vrijedi: $
\frac{|MT|}{|BM|} = \frac{|AC|}{|AB|}
$.
Iz ovog slijedi da je $|MT| = \frac{ab}{2\sqrt{a^2+b^2}}$.
Također vrijedi $|AM|=\sqrt{\frac{1}{4}a^2+b^2}$
$sin(\angle MAB) = \frac{|MT|}{|AM|} \leq \frac{1}{3}$
$\sqrt{\frac{1}{4}a^2+b^2} \geq \frac{3ab}{2\sqrt{a^2+b^2}}$
Kvadriranjem i sređivanjem dobijemo:
$a^4+4b^4 \geq 4a^2b^2$
$(a^2-2b^2) \geq 0$
Jednakost vrijedi kada je $a^2=2b^2$.
| 16. travnja 2012. 13:02 | Veki | Točno |
| 16. travnja 2012. 19:15 | grga | Točno |