Točno
6. studenoga 2016. 02:34 (8 godine)
Neka su
,
i
pozitivni realni brojevi za koje vrijedi
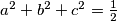
. Dokaži nejednakost
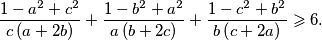
%V0
Neka su $a$, $b$ i $c$ pozitivni realni brojevi za koje vrijedi $a^2 + b^2 + c^2 = \frac{1}{2}$. Dokaži nejednakost $$ \frac{1 - a^2 + c^2}{c\left(a + 2 b\right)} + \frac{1 - b^2 + a^2}{a \left(b + 2 c\right)} + \frac{1 - c^2 + b^2}{b \left(c + 2 a\right)} \geqslant 6 \text{.} $$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
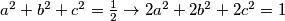
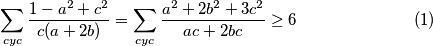
Primjenimo A-G na nazivnik izraza (1)
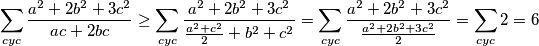
$a^2+b^2+c^2=\frac{1}{2}\rightarrow 2a^2+2b^2+2c^2=1$
\begin{equation}\label{1}
\sum_{cyc}\frac{1-a^2+c^2}{c(a+2b)}=\sum_{cyc}\frac{a^2+2b^2+3c^2}{ac+2bc}\geq 6
\end{equation}
Primjenimo A-G na nazivnik izraza (1)
$$\sum_{cyc}\frac{a^2+2b^2+3c^2}{ac+2bc}\geq \sum_{cyc}\frac{a^2+2b^2+3c^2}{\frac{a^2+c^2}{2}+b^2+c^2}=\sum_{cyc}\frac{a^2+2b^2+3c^2}{\frac{a^2+2b^2+3c^2}{2}}=\sum_{cyc}2=6$$
Školjka