Točno
16. travnja 2012. 07:49 (12 godine, 7 mjeseci)
Dani su realni brojevi
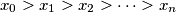
. Dokaži da je
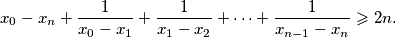
Kada vrijedi jednakost?
%V0
Dani su realni brojevi $x_{0} > x_{1} > x_{2} > \cdots > x_{n}$. Dokaži da je $$ x_{0} - x_{n} + \frac{1}{x_{0} - x_{1}} + \frac{1}{x_{1} - x_{2}} + \cdots + \frac{1}{x_{n - 1} - x_{n}} \geqslant 2n \text{.} $$
Kada vrijedi jednakost?
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Razliku
možemo prikazati kao
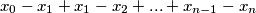
i koristeći činjenicu da
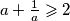
spariti svaki
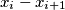
s
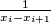
, kakvih imamo
, pa je suma očito veća od
Jednakost se postiže kada vrijedi
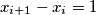
za svaki
%V0
Razliku $ x_0 - x_n $ možemo prikazati kao $ x_0 - x_1 + x_1 - x_2 + ... + x_{n-1} - x_n $ i koristeći činjenicu da $ a + \frac{1}{a} \geqslant 2 $ spariti svaki $ x_i - x_{i+1} $ s $\frac{1}{x_i-x_{i+1}}$, kakvih imamo $n$, pa je suma očito veća od $2n$
Jednakost se postiže kada vrijedi $ x_{i+1} - x_i =1 $ za svaki $i$
| 18. travnja 2012. 21:18 | ikicic | Točno |
Školjka