Neka su

,

,

realni brojevi i neka je
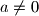
. Dokaži da barem jedna od jednadžbi
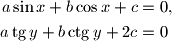
ima realna rješenja.
%V0
Neka su $a$, $b$, $c$ realni brojevi i neka je $a\neq 0$. Dokaži da barem jedna od jednadžbi $$$\begin{align*}
a\sin{x}+b\cos{x}+c&=0, \\
a\tg{y}+ b\ctg{y}+2c&=0
\end{align*}$$$ ima realna rješenja.