Duljine dviju stranica trokuta su

i

, njima nasuprotni kutovi su

i

, a visina na treću stranicu ima duljinu

.

Ako za kutove vrijedi
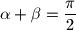
ili
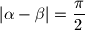
, dokaži da je
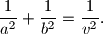

Ako ova jednakost vrijedi za neki trokut, dokaži da za njegove kutove vrijedi
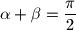
ili
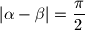
.
%V0
Duljine dviju stranica trokuta su $a$ i $b$, njima nasuprotni kutovi su $\alpha$ i $\beta$, a visina na treću stranicu ima duljinu $v$.
$a)$ Ako za kutove vrijedi $\alpha + \beta = \dfrac \pi 2$ ili $|\alpha - \beta| = \dfrac \pi 2$, dokaži da je $$
\frac1{a^2}+\frac1{b^2}=\frac1{v^2}.
$$
$b)$ Ako ova jednakost vrijedi za neki trokut, dokaži da za njegove kutove vrijedi $\alpha + \beta = \dfrac \pi 2$ ili $|\alpha - \beta| = \dfrac \pi 2$.