Neka je
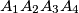
konveksan četverokut,

sjecište njegovih dijagonala. Označimo sa
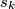
površinu trokuta
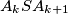
, (
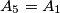
),
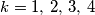
. Dokažite da je

ako i samo ako je
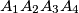
paralelogram.
%V0
Neka je $A_1A_2A_3A_4$ konveksan četverokut, $S$ sjecište njegovih dijagonala. Označimo sa $s_k$ površinu trokuta $A_kSA_{k+1}$, ($A_5 = A_1$), $k=1,\,2,\,3,\,4$. Dokažite da je $$s_2^2 = s_1s_3 \qquad \text{i} \qquad 2s_4=s_1+s_3$$ ako i samo ako je $A_1A_2A_3A_4$ paralelogram.