In a given right triangle

, the hypotenuse

, of length

, is divided into

equal parts (

and odd integer). Let
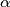
be the acute angel subtending, from

, that segment which contains the mdipoint of the hypotenuse. Let

be the length of the altitude to the hypotenuse fo the triangle. Prove that:
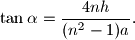
%V0
In a given right triangle $ABC$, the hypotenuse $BC$, of length $a$, is divided into $n$ equal parts ($n$ and odd integer). Let $\alpha$ be the acute angel subtending, from $A$, that segment which contains the mdipoint of the hypotenuse. Let $h$ be the length of the altitude to the hypotenuse fo the triangle. Prove that: $$\tan{\alpha}=\dfrac{4nh}{(n^2-1)a}.$$