Slični zadaci
Consider 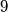 points in space, no four of which are coplanar. Each pair of points is joined by an edge (that is, a line segment) and each edge is either colored blue or red or left uncolored. Find the smallest value of
points in space, no four of which are coplanar. Each pair of points is joined by an edge (that is, a line segment) and each edge is either colored blue or red or left uncolored. Find the smallest value of  such that whenever exactly
such that whenever exactly  edges are colored, the set of colored edges necessarily contains a triangle all of whose edges have the same color.
edges are colored, the set of colored edges necessarily contains a triangle all of whose edges have the same color.
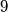 points in space, no four of which are coplanar. Each pair of points is joined by an edge (that is, a line segment) and each edge is either colored blue or red or left uncolored. Find the smallest value of
points in space, no four of which are coplanar. Each pair of points is joined by an edge (that is, a line segment) and each edge is either colored blue or red or left uncolored. Find the smallest value of  such that whenever exactly
such that whenever exactly  edges are colored, the set of colored edges necessarily contains a triangle all of whose edges have the same color.
edges are colored, the set of colored edges necessarily contains a triangle all of whose edges have the same color.  Školjka
Školjka  , given
, given 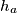 ,
, 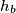 (the altitudes from
(the altitudes from  and
and  ), and
), and 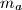 , the median from vertex
, the median from vertex  ,
,  and
and  be the lengths of the sides of a triangle. Prove that
be the lengths of the sides of a triangle. Prove that 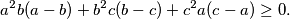
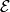 the set of all points contained in the three segments
the set of all points contained in the three segments  ,
,  , and
, and  (including
(including  ). Determine whether, for every partition of
). Determine whether, for every partition of  inside a given triangle
inside a given triangle  ,
,  ,
,  be the feet of the perpendiculars from the point
be the feet of the perpendiculars from the point 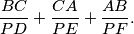
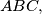 in its exterior
in its exterior we draw the triangles
we draw the triangles 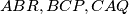 so that
so that 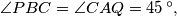
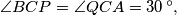
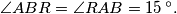
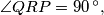 and
and 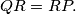
 be real numbers. Consider the quadratic equation in
be real numbers. Consider the quadratic equation in 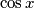
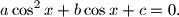 Using the numbers
Using the numbers 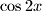 whose roots are the same as those of the original equation. Compare the equation in
whose roots are the same as those of the original equation. Compare the equation in 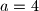 ,
,  ,
, 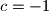 .
.