In an

-gon
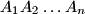
, all of whose interior angles are equal, the lengths of consecutive sides satisfy the relation
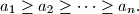
Prove that
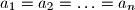
.
%V0
In an $n$-gon $A_{1}A_{2}\ldots A_{n}$, all of whose interior angles are equal, the lengths of consecutive sides satisfy the relation
$$a_{1}\geq a_{2}\geq \dots \geq a_{n}.$$
Prove that $a_{1}=a_{2}= \ldots= a_{n}$.