Slični zadaci
Pravilnom peterokutu povučene su sve dijagonale. Od  likova s najmanjom površinom na slici, "središnji" peterokut ima površinu
likova s najmanjom površinom na slici, "središnji" peterokut ima površinu  , svaki od
, svaki od  međusobno sukladnih šiljastokutnih trokuta ima površinu
međusobno sukladnih šiljastokutnih trokuta ima površinu  , te svaki od
, te svaki od  međusobno sukladnih tupokutnih trokuta ima površinu
međusobno sukladnih tupokutnih trokuta ima površinu  . ako je zadana površina
. ako je zadana površina  , nađite površine
, nađite površine  i
i  , te površinu cijelog peterokuta.
, te površinu cijelog peterokuta.
{{ Greška pri preuzimanju img datoteke. (Nevaljan broj?) }}
 likova s najmanjom površinom na slici, "središnji" peterokut ima površinu
likova s najmanjom površinom na slici, "središnji" peterokut ima površinu  , svaki od
, svaki od  međusobno sukladnih šiljastokutnih trokuta ima površinu
međusobno sukladnih šiljastokutnih trokuta ima površinu  , te svaki od
, te svaki od  međusobno sukladnih tupokutnih trokuta ima površinu
međusobno sukladnih tupokutnih trokuta ima površinu  . ako je zadana površina
. ako je zadana površina  , nađite površine
, nađite površine  i
i  , te površinu cijelog peterokuta.
, te površinu cijelog peterokuta.{{ Greška pri preuzimanju img datoteke. (Nevaljan broj?) }}
 Školjka
Školjka  i
i  kvadrata
kvadrata  izabrane su točke
izabrane su točke  i
i  , tim redom, takve da je
, tim redom, takve da je 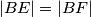 . Neka je
. Neka je 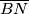 visina trokuta
visina trokuta 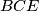 . Dokažite da je trokut
. Dokažite da je trokut 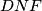 pravokutan.
pravokutan. 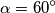 ,
, 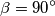 ,
, 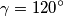 . Dijagonale
. Dijagonale  i
i  sijeku se u točki
sijeku se u točki  , pri čemu je
, pri čemu je 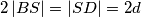 . Iz polovišta
. Iz polovišta  dijagonale
dijagonale 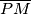 na dijagonalu
na dijagonalu 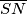 na
na 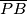 .
.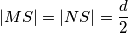
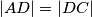
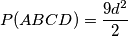 .
.  nalazi se točka
nalazi se točka  je unutar kvadrata
je unutar kvadrata  ,
,  ,
,  ,
, 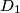 druge točke presjeka pravaca
druge točke presjeka pravaca 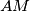 ,
, 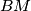 ,
, 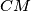 ,
, 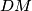 , tim redom, s kružnicom opisanom kvadratu
, tim redom, s kružnicom opisanom kvadratu 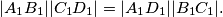
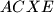 i
i 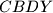 . Dokažite da se pravci
. Dokažite da se pravci  i
i  sijeku na visini iz vrha
sijeku na visini iz vrha  trokuta
trokuta  i
i  . ako je
. ako je 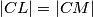 , dokazite da je
, dokazite da je 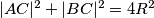 , gdje je
, gdje je  duljina polumjera kruznice opisane trokutu
duljina polumjera kruznice opisane trokutu