Given
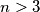
points in the plane such that no three of the points are collinear. Does there exist a circle passing through (at least)

of the given points and not containing any other of the

points in its interior ?
%V0
Given $n>3$ points in the plane such that no three of the points are collinear. Does there exist a circle passing through (at least) $3$ of the given points and not containing any other of the $n$ points in its interior ?