Školjka A regular triangular prism has the altitude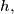 
and the two bases of the prism are equilateral triangles with side length 
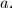Dream-holes are made in the centers of both bases, and the three lateral faces are mirrors. Assume that a ray of light, entering the prism through the dream-hole in the upper base, then being reflected once by any of the three mirrors, quits the prism through the dream-hole in the lower base. Find the angle between the upper base and the light ray at the moment when the light ray entered the prism, and the length of the way of the light ray in the interior of the prism.
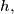and the two bases of the prism are equilateral triangles with side length 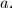Dream-holes are made in the centers of both bases, and the three lateral faces are mirrors. Assume that a ray of light, entering the prism through the dream-hole in the upper base, then being reflected once by any of the three mirrors, quits the prism through the dream-hole in the lower base. Find the angle between the upper base and the light ray at the moment when the light ray entered the prism, and the length of the way of the light ray in the interior of the prism.