Given

points in the plane, no three of them being collinear. Show that among these

points, we can always find
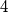
points forming a convex quadrilateral.
%V0
Given $5$ points in the plane, no three of them being collinear. Show that among these $5$ points, we can always find $4$ points forming a convex quadrilateral.