Given three congruent rectangles in the space. Their centers coincide, but the planes they lie in are mutually perpendicular. For any two of the three rectangles, the line of intersection of the planes of these two rectangles contains one midparallel of one rectangle and one midparallel of the other rectangle, and these two midparallels have different lengths. Consider the convex polyhedron whose vertices are the vertices of the rectangles.
a.) What is the volume of this polyhedron ?
b.) Can this polyhedron turn out to be a regular polyhedron ? If yes, what is the condition for this polyhedron to be regular ?
a.) What is the volume of this polyhedron ?
b.) Can this polyhedron turn out to be a regular polyhedron ? If yes, what is the condition for this polyhedron to be regular ?
Slični zadaci
Let  be a finite set of points such that
be a finite set of points such that  is not contained in a plane and no three points of
is not contained in a plane and no three points of  are collinear. Show that at least one of the following alternatives holds:
are collinear. Show that at least one of the following alternatives holds:
(i) contains five points that are vertices of a convex pyramid having no other points in common with
contains five points that are vertices of a convex pyramid having no other points in common with 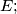
(ii) some plane contains exactly three points from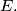
 be a finite set of points such that
be a finite set of points such that  is not contained in a plane and no three points of
is not contained in a plane and no three points of  are collinear. Show that at least one of the following alternatives holds:
are collinear. Show that at least one of the following alternatives holds:(i)
 contains five points that are vertices of a convex pyramid having no other points in common with
contains five points that are vertices of a convex pyramid having no other points in common with 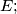
(ii) some plane contains exactly three points from
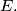
Let  and
and 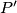 be two parallelograms with equal area, and let their sidelengths be
be two parallelograms with equal area, and let their sidelengths be 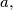
 and
and 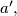
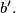 Assume that
Assume that 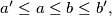 and moreover, it is possible to place the segment
and moreover, it is possible to place the segment 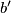 such that it completely lies in the interior of the parallelogram
such that it completely lies in the interior of the parallelogram 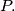
Show that the parallelogram can be partitioned into four polygons such that these four polygons can be composed again to form the parallelogram
can be partitioned into four polygons such that these four polygons can be composed again to form the parallelogram 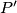 .
.
 and
and 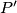 be two parallelograms with equal area, and let their sidelengths be
be two parallelograms with equal area, and let their sidelengths be 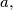
 and
and 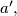
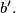 Assume that
Assume that 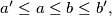 and moreover, it is possible to place the segment
and moreover, it is possible to place the segment 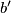 such that it completely lies in the interior of the parallelogram
such that it completely lies in the interior of the parallelogram 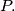
Show that the parallelogram
 can be partitioned into four polygons such that these four polygons can be composed again to form the parallelogram
can be partitioned into four polygons such that these four polygons can be composed again to form the parallelogram 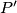 .
.  Školjka
Školjka  be a convex quadrilateral
be a convex quadrilateral  and
and  a point inside it. The feet of the perpendiculars from
a point inside it. The feet of the perpendiculars from 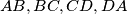 are
are 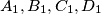 respectively. The feet of the perpendiculars from
respectively. The feet of the perpendiculars from 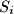 , the quadrilateral
, the quadrilateral 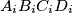 , are
, are 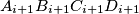 , where
, where 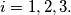 Prove that
Prove that 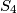 is similar to S.
is similar to S. 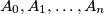 be points in a plane such that
be points in a plane such that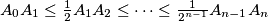 and
and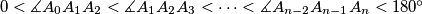 ,
,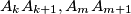 do not intersect for each
do not intersect for each  and
and  such that
such that 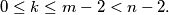
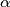 . There is a candle inside the angle. How many reflections of the candle can an observer see?
. There is a candle inside the angle. How many reflections of the candle can an observer see?  points in the plane, no three of them being collinear. Show that among these
points in the plane, no three of them being collinear. Show that among these 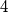 points forming a convex quadrilateral.
points forming a convex quadrilateral.