Prove that the volume
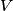
and the lateral area
of a right circular cone satisfy the inequality
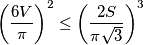
When does equality occur?
%V0
Prove that the volume $V$ and the lateral area $S$ of a right circular cone satisfy the inequality
$$\left( \frac{6V}{\pi}\right)^2 \leq \left( \frac{2S}{\pi \sqrt 3}\right)^3$$
When does equality occur?
Školjka