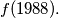Slični zadaci
neka je 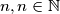 , te
, te 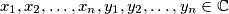
postoji li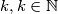 , takav da se iz jednakosti
, takav da se iz jednakosti 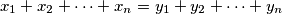
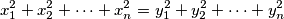

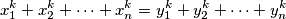
moze zakljuciti da su " -evi" do na permutaciju jednaki "
-evi" do na permutaciju jednaki " -ima". ako postoji, koji je najmanji takav
-ima". ako postoji, koji je najmanji takav  .
.
dodatno, postoji li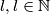 takav da se za proizvoljnih
takav da se za proizvoljnih  brojeva
brojeva 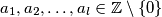 , takvih da
, takvih da 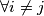 vrijedi
vrijedi 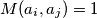 te odgovarajucih jednakosti
te odgovarajucih jednakosti
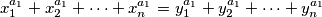
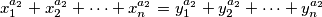

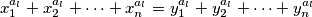
moze zakljuciti da su " -evi" do na permutaciju jednaki "
-evi" do na permutaciju jednaki " -ima". ako postoji, koji je najmanji takav
-ima". ako postoji, koji je najmanji takav  .
.
takoder, uz pretpostavku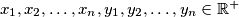 , smijemo li uzeti
, smijemo li uzeti 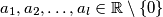 ?
?
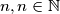 , te
, te 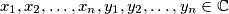
postoji li
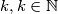 , takav da se iz jednakosti
, takav da se iz jednakosti 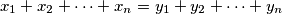
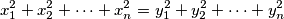

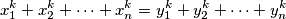
moze zakljuciti da su "
 -evi" do na permutaciju jednaki "
-evi" do na permutaciju jednaki " -ima". ako postoji, koji je najmanji takav
-ima". ako postoji, koji je najmanji takav  .
.dodatno, postoji li
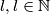 takav da se za proizvoljnih
takav da se za proizvoljnih  brojeva
brojeva 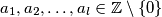 , takvih da
, takvih da 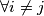 vrijedi
vrijedi 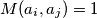 te odgovarajucih jednakosti
te odgovarajucih jednakosti 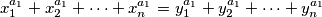
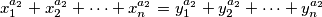

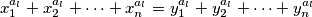
moze zakljuciti da su "
 -evi" do na permutaciju jednaki "
-evi" do na permutaciju jednaki " -ima". ako postoji, koji je najmanji takav
-ima". ako postoji, koji je najmanji takav  .
.takoder, uz pretpostavku
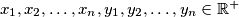 , smijemo li uzeti
, smijemo li uzeti 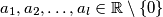 ?
? 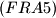 Let
Let 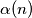 be the number of pairs
be the number of pairs 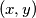 of integers such that
of integers such that 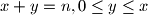 , and let
, and let 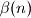 be the number of triples
be the number of triples 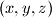 such that
such that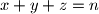 and
and 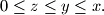 Find a simple relation between
Find a simple relation between 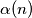 and the integer part of the number
and the integer part of the number 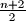 and the relation among
and the relation among 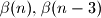 and
and 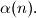 Then evaluate
Then evaluate 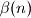 as a function of the residue of
as a function of the residue of  modulo
modulo  . What can be said about
. What can be said about 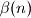 and
and 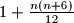 ? And what about
? And what about 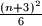 ?
? Find the number of triples
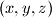 with the property
with the property 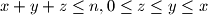 as a function of the residue of
as a function of the residue of  modulo
modulo 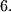 What can be said about the relation between this number and the number
What can be said about the relation between this number and the number 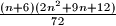 ?
?  Školjka
Školjka 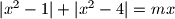 as a function of the parameter
as a function of the parameter  . Which pairs
. Which pairs 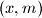 of integers satisfy this equation ?
of integers satisfy this equation ? 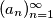 be a sequence of integers with
be a sequence of integers with 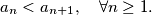 For all quadruple
For all quadruple 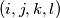 of indices such that
of indices such that 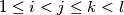 and
and 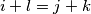 we have the inequality
we have the inequality 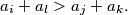 Determine the least possible value of
Determine the least possible value of 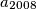 .
.  and
and 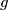 be two integer-valued functions defined on the set of all integers such that
be two integer-valued functions defined on the set of all integers such that 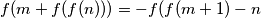 for all integers
for all integers 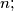
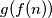
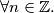
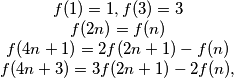
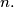 Determine with proof the number of positive integers
Determine with proof the number of positive integers 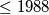 for which
for which 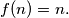
 be a function defined on the set of all positive integers and having its values in the same set. Suppose that
be a function defined on the set of all positive integers and having its values in the same set. Suppose that 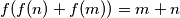 for all positive integers
for all positive integers 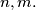 Find the possible value for
Find the possible value for