The side lengths
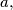
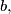

of a triangle

form an arithmetical progression (such that
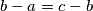
). The side lengths
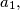
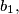
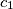
of a triangle
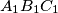
also form an arithmetical progression (with
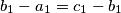
). (Hereby,
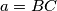
,
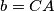
,
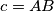
,
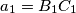
,
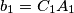
,
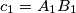
.) Moreover, we know that
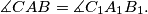
Show that triangles

and
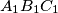
are similar.
%V0
The side lengths $a,$ $b,$ $c$ of a triangle $ABC$ form an arithmetical progression (such that $b-a=c-b$). The side lengths $a_{1},$ $b_{1},$ $c_{1}$ of a triangle $A_{1}B_{1}C_{1}$ also form an arithmetical progression (with $b_{1}-a_{1}=c_{1}-b_{1}$). (Hereby, $a=BC$, $b=CA$, $c=AB$, $a_{1}=B_{1}C_{1}$, $b_{1}=C_{1}A_{1}$, $c_{1}=A_{1}B_{1}$.) Moreover, we know that $\measuredangle CAB=\measuredangle C_{1}A_{1}B_{1}.$
Show that triangles $ABC$ and $A_{1}B_{1}C_{1}$ are similar.