Let
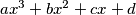
be a polynomial with integer coefficients
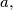
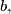
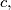

such that
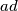
is an odd number and
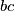
is an even number. Prove that (at least) one root of the polynomial is irrational.
%V0
Let $ax^{3}+bx^{2}+cx+d$ be a polynomial with integer coefficients $a,$ $b,$ $c,$ $d$ such that $ad$ is an odd number and $bc$ is an even number. Prove that (at least) one root of the polynomial is irrational.