An alphabet consists of

letters. What is the maximal length of a word if we know that any two consecutive letters
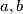
of the word are different and that the word cannot be reduced to a word of the kind
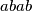
with
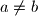
by removing letters.
%V0
An alphabet consists of $n$ letters. What is the maximal length of a word if we know that any two consecutive letters $a,b$ of the word are different and that the word cannot be reduced to a word of the kind $abab$ with $a\neq b$ by removing letters.