Prove that for every natural number

, and for every real number
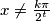
(
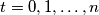
;

any integer)
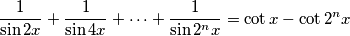
%V0
Prove that for every natural number $n$, and for every real number $x \neq \frac{k\pi}{2^t}$ ($t=0,1, \dots, n$; $k$ any integer) $$\frac{1}{\sin{2x}}+\frac{1}{\sin{4x}}+\dots+\frac{1}{\sin{2^nx}}=\cot{x}-\cot{2^nx}$$