Let  be a triangle, and let
be a triangle, and let  ,
,  ,
,  be three points in the interiors of the sides
be three points in the interiors of the sides  ,
,  ,
,  of this triangle. Prove that the area of at least one of the three triangles
of this triangle. Prove that the area of at least one of the three triangles 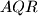 ,
, 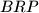 ,
, 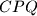 is less than or equal to one quarter of the area of triangle
is less than or equal to one quarter of the area of triangle  .
.
Alternative formulation: Let be a triangle, and let
be a triangle, and let  ,
,  ,
,  be three points on the segments
be three points on the segments  ,
,  ,
,  , respectively. Prove that
, respectively. Prove that
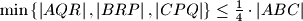 ,
,
where the abbreviation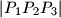 denotes the (non-directed) area of an arbitrary triangle
denotes the (non-directed) area of an arbitrary triangle 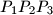 .
.
 be a triangle, and let
be a triangle, and let  ,
,  ,
,  be three points in the interiors of the sides
be three points in the interiors of the sides  ,
,  ,
,  of this triangle. Prove that the area of at least one of the three triangles
of this triangle. Prove that the area of at least one of the three triangles 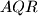 ,
, 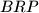 ,
, 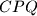 is less than or equal to one quarter of the area of triangle
is less than or equal to one quarter of the area of triangle  .
. Alternative formulation: Let
 be a triangle, and let
be a triangle, and let  ,
,  ,
,  be three points on the segments
be three points on the segments  ,
,  ,
,  , respectively. Prove that
, respectively. Prove that 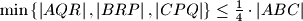 ,
, where the abbreviation
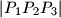 denotes the (non-directed) area of an arbitrary triangle
denotes the (non-directed) area of an arbitrary triangle 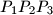 .
.  Školjka
Školjka