Prove that
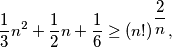
and let
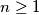
be an integer. Prove that this inequality is only possible in the case
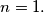
%V0
Prove that
$$\frac{1}{3}n^2 + \frac{1}{2}n + \frac{1}{6} \geq (n!)^{\dfrac{2}{n}},$$
and let $n \geq 1$ be an integer. Prove that this inequality is only possible in the case $n = 1.$