Let

be natural numbers such that
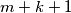
is a prime greater than
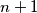
. Let
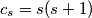
. Prove that
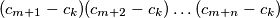
is divisible by the product
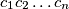
.
%V0
Let $k,m,n$ be natural numbers such that $m+k+1$ is a prime greater than $n+1$. Let $c_s=s(s+1)$. Prove that
$$(c_{m+1}-c_k)(c_{m+2}-c_k)\ldots(c_{m+n}-c_k)$$
is divisible by the product $c_1c_2\ldots c_n$.