The

points
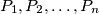
are placed inside or on the boundary of a disk of radius 1 in such a way that the minimum distance
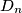
between any two of these points has its largest possible value
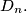
Calculate
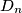
for
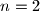
to 7. and justify your answer.
%V0
The $n$ points $P_1,P_2, \ldots, P_n$ are placed inside or on the boundary of a disk of radius 1 in such a way that the minimum distance $D_n$ between any two of these points has its largest possible value $D_n.$ Calculate $D_n$ for $n = 2$ to 7. and justify your answer.