Prove that for an arbitrary pair of vectors

and

in the space the inequality
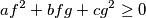
holds if and only if the following conditions are fulfilled:
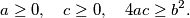
%V0
Prove that for an arbitrary pair of vectors $f$ and $g$ in the space the inequality
$$af^2 + bfg +cg^2 \geq 0$$
holds if and only if the following conditions are fulfilled:
$$a \geq 0, \quad c \geq 0, \quad 4ac \geq b^2.$$