Let

be a regular tetrahedron. To an arbitrary point

on one edge, say

, corresponds the point
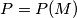
which is the intersection of two lines
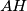
and
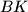
, drawn from

orthogonally to
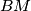
and from

orthogonally to
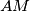
. What is the locus of

when

varies ?
%V0
Let $ABCD$ be a regular tetrahedron. To an arbitrary point $M$ on one edge, say $CD$, corresponds the point $P = P(M)$ which is the intersection of two lines $AH$ and $BK$, drawn from $A$ orthogonally to $BM$ and from $B$ orthogonally to $AM$. What is the locus of $P$ when $M$ varies ?