A line

is drawn through the intersection point

of altitudes of acute-angle triangles. Prove that symmetric images
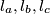
of

with respect to the sides
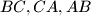
have one point in common, which lies on the circumcircle of

%V0
A line $l$ is drawn through the intersection point $H$ of altitudes of acute-angle triangles. Prove that symmetric images $l_a, l_b, l_c$ of $l$ with respect to the sides $BC,CA,AB$ have one point in common, which lies on the circumcircle of $ABC.$