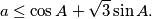Slični zadaci
Let  be an acute-angled triangle. The lines
be an acute-angled triangle. The lines 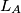 ,
, 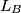 and
and 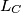 are constructed through the vertices
are constructed through the vertices  ,
,  and
and  respectively according the following prescription: Let
respectively according the following prescription: Let  be the foot of the altitude drawn from the vertex
be the foot of the altitude drawn from the vertex  to the side
to the side  ; let
; let 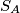 be the circle with diameter
be the circle with diameter 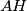 ; let
; let 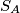 meet the sides
meet the sides  and
and  at
at  and
and  respectively, where
respectively, where  and
and  are distinct from
are distinct from  ; then let
; then let 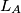 be the line through
be the line through  perpendicular to
perpendicular to  . The lines
. The lines 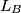 and
and 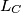 are constructed similarly. Prove that the lines
are constructed similarly. Prove that the lines 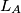 ,
, 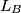 and
and 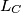 are concurrent.
are concurrent.
 be an acute-angled triangle. The lines
be an acute-angled triangle. The lines 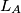 ,
, 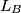 and
and 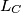 are constructed through the vertices
are constructed through the vertices  ,
,  and
and  respectively according the following prescription: Let
respectively according the following prescription: Let  be the foot of the altitude drawn from the vertex
be the foot of the altitude drawn from the vertex  to the side
to the side  ; let
; let 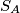 be the circle with diameter
be the circle with diameter 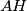 ; let
; let 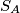 meet the sides
meet the sides  and
and  at
at  and
and  respectively, where
respectively, where  and
and  are distinct from
are distinct from  ; then let
; then let 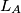 be the line through
be the line through  perpendicular to
perpendicular to  . The lines
. The lines 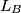 and
and 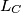 are constructed similarly. Prove that the lines
are constructed similarly. Prove that the lines 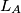 ,
, 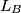 and
and 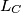 are concurrent.
are concurrent.  Školjka
Školjka  is drawn through the intersection point
is drawn through the intersection point 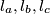 of
of 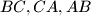 have one point in common, which lies on the circumcircle of
have one point in common, which lies on the circumcircle of 
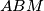 and
and 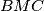 are equal. Prove that
are equal. Prove that 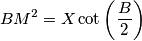
 be the centre of the inscribed circle of a triangle
be the centre of the inscribed circle of a triangle 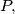
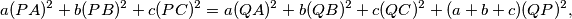
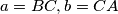 and
and 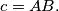
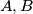 and
and 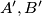 and
and 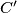 respectively. Prove that the area of triangle
respectively. Prove that the area of triangle 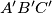 is greater than or equal to the area of triangle
is greater than or equal to the area of triangle  and its diameter
and its diameter 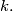
 has
has 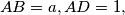
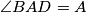 , and the triangle
, and the triangle 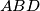 has all angles acute. Prove that circles radius
has all angles acute. Prove that circles radius  and center
and center 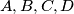 cover the parallelogram if and only
cover the parallelogram if and only