The equation
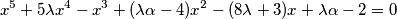
is given. Determine
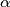
so that the given equation has exactly (i) one root or (ii) two roots, respectively, independent from
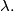
%V0
The equation
$$x^5 + 5 \lambda x^4 - x^3 + (\lambda \alpha - 4)x^2 - (8 \lambda + 3)x + \lambda \alpha - 2 = 0$$
is given. Determine $\alpha$ so that the given equation has exactly (i) one root or (ii) two roots, respectively, independent from $\lambda.$
Školjka