If
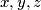
are real numbers satisfying relations
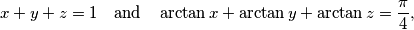
prove that
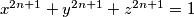
holds for all positive integers

.
%V0
If $x,y,z$ are real numbers satisfying relations
$$x+y+z = 1 \quad \textrm{and} \quad \arctan x + \arctan y + \arctan z = \frac{\pi}{4},$$
prove that $x^{2n+1} + y^{2n+1} + z^{2n+1} = 1$ holds for all positive integers $n$.