Let

be real numbers with

non-zero. It is known that the real numbers
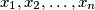
satisfy the

equations:
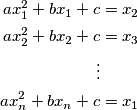
Prove that the system has zero, one or more than one real solutions if
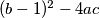
is negative, equal to zero or positive respectively.
%V0
Let $a,b,c$ be real numbers with $a$ non-zero. It is known that the real numbers $x_1,x_2,\ldots,x_n$ satisfy the $n$ equations:$$$\begin{align*}
ax_1^2+bx_1+c &= x_{2} \\
ax_2^2+bx_2 +c &= x_3 \\
\vdots \\
ax_n^2+bx_n+c &= x_1
\end{align*}$$$
Prove that the system has zero, one or more than one real solutions if $(b-1)^2-4ac$ is negative, equal to zero or positive respectively.