If
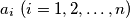
are distinct non-zero real numbers, prove that the equation
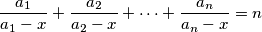
has at least
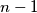
real roots.
%V0
If $a_i \ (i = 1, 2, \ldots, n)$ are distinct non-zero real numbers, prove that the equation
$$\frac{a_1}{a_1-x} + \frac{a_2}{a_2-x}+\cdots+\frac{a_n}{a_n-x} = n$$
has at least $n - 1$ real roots.