Given two congruent triangles
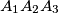
and
(
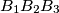
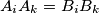
), prove that there exists a plane such that the orthogonal projections of these triangles onto it are congruent and equally oriented.
%V0
Given two congruent triangles $A_1A_2A_3$ and $B_1B_2B_3$ ($A_iA_k = B_iB_k$), prove that there exists a plane such that the orthogonal projections of these triangles onto it are congruent and equally oriented.
Školjka