Given

parallel lines
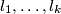
and
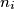
points on the line
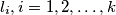
, find the maximum possible number of triangles with vertices at these points.
%V0
Given $k$ parallel lines $l_1, \ldots, l_k$ and $n_i$ points on the line $l_i, i = 1, 2, \ldots, k$, find the maximum possible number of triangles with vertices at these points.