Slični zadaci
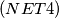 A boy has a set of trains and pieces of railroad track. Each piece is a quarter of circle, and by concatenating these pieces, the boy obtained a closed railway. The railway does not intersect itself. In passing through this railway, the train sometimes goes in the clockwise direction, and sometimes in the opposite direction. Prove that the train passes an even number of times through the pieces in the clockwise direction and an even number of times in the counterclockwise direction. Also, prove that the number of pieces is divisible by
A boy has a set of trains and pieces of railroad track. Each piece is a quarter of circle, and by concatenating these pieces, the boy obtained a closed railway. The railway does not intersect itself. In passing through this railway, the train sometimes goes in the clockwise direction, and sometimes in the opposite direction. Prove that the train passes an even number of times through the pieces in the clockwise direction and an even number of times in the counterclockwise direction. Also, prove that the number of pieces is divisible by 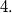
 Školjka
Školjka  Construct the circle that is tangent to three given circles.
Construct the circle that is tangent to three given circles. 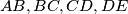 with lengths
with lengths 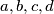 , respectively, are given. Prove that
, respectively, are given. Prove that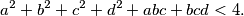
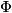 in the plane any two points of which are connectable by a semicircle lying in
in the plane any two points of which are connectable by a semicircle lying in 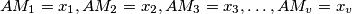 , such that
, such that 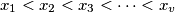 . Prove that
. Prove that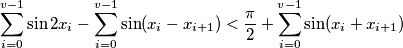
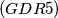 Given a ring
Given a ring  in the plane bounded by two concentric circles with radii
in the plane bounded by two concentric circles with radii  and
and 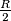 , prove that we can cover this region with
, prove that we can cover this region with 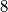 disks of radius
disks of radius 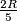 . (A region is covered if each of its points is inside or on the border of some disk.)
. (A region is covered if each of its points is inside or on the border of some disk.)