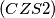
Let

be a prime odd number. Is it possible to find
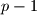
natural numbers
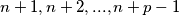
such that the sum of the squares of these numbers is divisible by the sum of these numbers?
%V0
$(CZS 2)$ Let $p$ be a prime odd number. Is it possible to find $p-1$ natural numbers $n + 1, n + 2, . . . , n + p -1$ such that the sum of the squares of these numbers is divisible by the sum of these numbers?