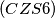
Let
and
be two real numbers. Find the first term of an arithmetic progression
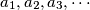
with difference
such that
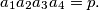
Find the number of solutions in terms of
and
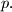
%V0
$(CZS 6)$ Let $d$ and $p$ be two real numbers. Find the first term of an arithmetic progression $a_1, a_2, a_3, \cdots$ with difference $d$ such that $a_1a_2a_3a_4 = p.$ Find the number of solutions in terms of $d$ and $p.$
Školjka