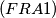
Let

and

be two nonnegative integers. Denote by
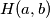
the set of numbers

of the form
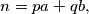
where

and

are positive integers. Determine
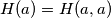
. Prove that if
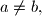
it is enough to know all the sets
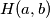
for coprime numbers
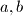
in order to know all the sets
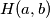
. Prove that in the case of coprime numbers

and
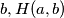
contains all numbers greater than or equal to
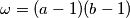
and also
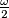
numbers smaller than

%V0
$(FRA 1)$ Let $a$ and $b$ be two nonnegative integers. Denote by $H(a, b)$ the set of numbers $n$ of the form $n = pa + qb,$ where $p$ and $q$ are positive integers. Determine $H(a) = H(a, a)$. Prove that if $a \neq b,$ it is enough to know all the sets $H(a, b)$ for coprime numbers $a, b$ in order to know all the sets $H(a, b)$. Prove that in the case of coprime numbers $a$ and $b, H(a, b)$ contains all numbers greater than or equal to $\omega = (a - 1)(b -1)$ and also $\frac{\omega}{2}$ numbers smaller than $\omega$
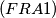 Let
Let  and
and  be two nonnegative integers. Denote by
be two nonnegative integers. Denote by 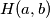 the set of numbers
the set of numbers  of the form
of the form 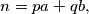 where
where  and
and  are positive integers. Determine
are positive integers. Determine 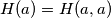 . Prove that if
. Prove that if 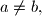 it is enough to know all the sets
it is enough to know all the sets 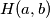 for coprime numbers
for coprime numbers 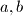 in order to know all the sets
in order to know all the sets 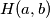 . Prove that in the case of coprime numbers
. Prove that in the case of coprime numbers  and
and 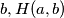 contains all numbers greater than or equal to
contains all numbers greater than or equal to 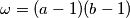 and also
and also 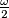 numbers smaller than
numbers smaller than 
 Školjka
Školjka