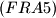
Let
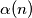
be the number of pairs
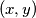
of integers such that
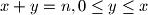
, and let
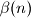
be the number of triples
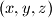
such that
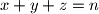
and
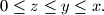
Find a simple relation between
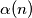
and the integer part of the number
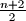
and the relation among
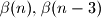
and
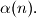
Then evaluate
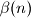
as a function of the residue of

modulo
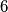
. What can be said about
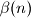
and
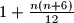
? And what about
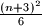
?
Find the number of triples
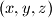
with the property
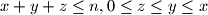
as a function of the residue of

modulo
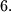
What can be said about the relation between this number and the number
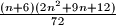
?
%V0
$(FRA 5)$ Let $\alpha(n)$ be the number of pairs $(x, y)$ of integers such that $x+y = n, 0 \le y \le x$, and let $\beta(n)$ be the number of triples $(x, y, z)$ such that$x + y + z = n$ and $0 \le z \le y \le x.$ Find a simple relation between $\alpha(n)$ and the integer part of the number $\frac{n+2}{2}$ and the relation among $\beta(n), \beta(n -3)$ and $\alpha(n).$ Then evaluate $\beta(n)$ as a function of the residue of $n$ modulo $6$. What can be said about $\beta(n)$ and $1+\frac{n(n+6)}{12}$? And what about $\frac{(n+3)^2}{6}$?
Find the number of triples $(x, y, z)$ with the property $x+ y+ z \le n, 0 \le z \le y \le x$ as a function of the residue of $n$ modulo $6.$What can be said about the relation between this number and the number $\frac{(n+6)(2n^2+9n+12)}{72}$?
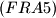 Let
Let 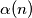 be the number of pairs
be the number of pairs 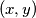 of integers such that
of integers such that 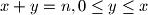 , and let
, and let 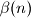 be the number of triples
be the number of triples 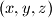 such that
such that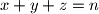 and
and 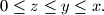 Find a simple relation between
Find a simple relation between 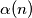 and the integer part of the number
and the integer part of the number 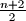 and the relation among
and the relation among 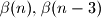 and
and 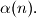 Then evaluate
Then evaluate 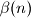 as a function of the residue of
as a function of the residue of  modulo
modulo 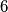 . What can be said about
. What can be said about 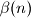 and
and 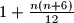 ? And what about
? And what about 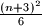 ?
? 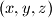 with the property
with the property 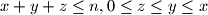 as a function of the residue of
as a function of the residue of  modulo
modulo 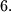 What can be said about the relation between this number and the number
What can be said about the relation between this number and the number 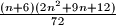 ?
?  Školjka
Školjka