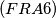
Consider the integer
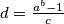
, where
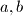
, and

are positive integers and
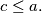
Prove that the set

of integers that are between

and

and relatively prime to

(the number of such integers is denoted by
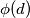
) can be partitioned into

subsets, each of which consists of

elements. What can be said about the rational number
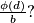
%V0
$(FRA 6)$ Consider the integer $d = \frac{a^b-1}{c}$, where $a, b$, and $c$ are positive integers and $c \le a.$ Prove that the set $G$ of integers that are between $1$ and $d$ and relatively prime to $d$ (the number of such integers is denoted by $\phi(d)$) can be partitioned into $n$ subsets, each of which consists of $b$ elements. What can be said about the rational number $\frac{\phi(d)}{b}?$