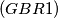
The polynomial
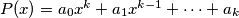
, where
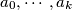
are integers, is said to be divisible by an integer

if

is a multiple of

for every integral value of

. Show that if

is divisible by

, then
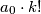
is a multiple of

. Also prove that if
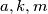
are positive integers such that
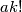
is a multiple of

, then a polynomial

with leading term
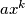
can be found that is divisible by

%V0
$(GBR 1)$ The polynomial $P(x) = a_0x^k + a_1x^{k-1} + \cdots + a_k$, where $a_0,\cdots, a_k$ are integers, is said to be divisible by an integer $m$ if $P(x)$ is a multiple of $m$ for every integral value of $x$. Show that if $P(x)$ is divisible by $m$, then $a_0 \cdot k!$ is a multiple of $m$. Also prove that if $a, k,m$ are positive integers such that $ak!$ is a multiple of $m$, then a polynomial $P(x)$ with leading term $ax^k$can be found that is divisible by $m.$
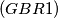 The polynomial
The polynomial 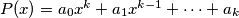 , where
, where 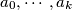 are integers, is said to be divisible by an integer
are integers, is said to be divisible by an integer  if
if  is a multiple of
is a multiple of  for every integral value of
for every integral value of  . Show that if
. Show that if  is divisible by
is divisible by  , then
, then 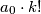 is a multiple of
is a multiple of  . Also prove that if
. Also prove that if 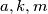 are positive integers such that
are positive integers such that 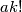 is a multiple of
is a multiple of  , then a polynomial
, then a polynomial  with leading term
with leading term 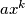 can be found that is divisible by
can be found that is divisible by 
 Školjka
Školjka