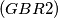
Let
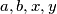
be positive integers such that

and

have no common divisor greater than
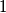
. Prove that the largest number not expressible in the form
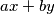
is
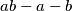
. If
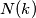
is the largest number not expressible in the form
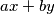
in only

ways, find
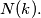
%V0
$(GBR 2)$ Let $a, b, x, y$ be positive integers such that $a$ and $b$ have no common divisor greater than $1$. Prove that the largest number not expressible in the form $ax + by$ is $ab - a - b$. If $N(k)$ is the largest number not expressible in the form $ax + by$ in only $k$ ways, find $N(k).$