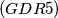
Given a ring

in the plane bounded by two concentric circles with radii

and
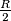
, prove that we can cover this region with
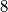
disks of radius
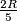
. (A region is covered if each of its points is inside or on the border of some disk.)
%V0
$(GDR 5)$ Given a ring $G$ in the plane bounded by two concentric circles with radii $R$ and $\frac{R}{2}$, prove that we can cover this region with $8$ disks of radius $\frac{2R}{5}$. (A region is covered if each of its points is inside or on the border of some disk.)