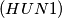
Let

and

be arbitrary integers. Prove that if

is an integer not divisible by

, then
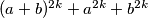
is divisible by
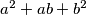
%V0
$(HUN 1)$ Let $a$ and $b$ be arbitrary integers. Prove that if $k$ is an integer not divisible by $3$, then $(a + b)^{2k}+ a^{2k} +b^{2k}$ is divisible by $a^2 +ab+ b^2$