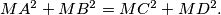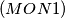 Find the number of five-digit numbers with the following properties: there are two pairs of digits such that digits from each pair are equal and are next to each other, digits from different pairs are different, and the remaining digit (which does not belong to any of the pairs) is different from the other digits.
Find the number of five-digit numbers with the following properties: there are two pairs of digits such that digits from each pair are equal and are next to each other, digits from different pairs are different, and the remaining digit (which does not belong to any of the pairs) is different from the other digits.  Školjka
Školjka 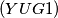 Suppose that positive real numbers
Suppose that positive real numbers 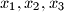 satisfy
satisfy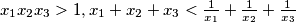
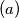 None of
None of  .
.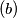 Exactly one of these numbers is less than
Exactly one of these numbers is less than 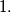
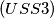
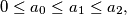 then
then 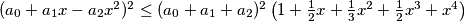
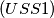 Prove that for a natural number
Prove that for a natural number ![n > 2, (n!)! > n[(n - 1)!]^{n!}.](/media/m/5/e/3/5e355a498babdb4f82fa93241266c77d.png)
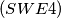 Let
Let 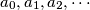 be determined with
be determined with 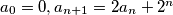 . Prove that if
. Prove that if  is power of
is power of  , then so is
, then so is 
 and
and  be two natural numbers that have an equal number
be two natural numbers that have an equal number  digits (from left to right) of the numbers
digits (from left to right) of the numbers 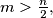 then
then 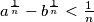
 Given two segments
Given two segments  and
and  not in the same plane, find the locus of points
not in the same plane, find the locus of points  such that
such that