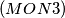
Let
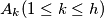
be
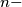
element sets such that each two of them have a nonempty intersection. Let

be the union of all the sets
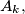
and let

be a subset of

such that for each
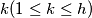
the intersection of
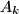
and

consists of exactly two different elements
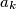
and
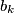
. Find all subsets

of the set

with

elements satisfying the condition that for at least one index
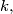
both elements
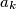
and
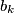
belong to

.
%V0
$(MON 3)$ Let $A_k (1 \le k \le h)$ be $n-$element sets such that each two of them have a nonempty intersection. Let $A$ be the union of all the sets $A_k,$ and let $B$ be a subset of $A$ such that for each $k (1\le k \le h)$ the intersection of $A_k$ and $B$ consists of exactly two different elements $a_k$ and $b_k$. Find all subsets $X$ of the set $A$ with $r$ elements satisfying the condition that for at least one index $k,$ both elements $a_k$ and $b_k$ belong to $X$.
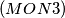 Let
Let 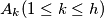 be
be 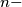 element sets such that each two of them have a nonempty intersection. Let
element sets such that each two of them have a nonempty intersection. Let  be the union of all the sets
be the union of all the sets 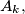 and let
and let  be a subset of
be a subset of  such that for each
such that for each 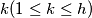 the intersection of
the intersection of 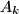 and
and  consists of exactly two different elements
consists of exactly two different elements 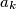 and
and 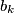 . Find all subsets
. Find all subsets  of the set
of the set  with
with  elements satisfying the condition that for at least one index
elements satisfying the condition that for at least one index 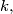 both elements
both elements 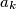 and
and 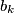 belong to
belong to  .
.  Školjka
Školjka