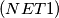
The vertices of an
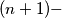
gon are placed on the edges of a regular
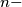
gon so that the perimeter of the
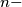
gon is divided into equal parts. How does one choose these

points in order to obtain the
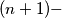
gon with
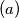
maximal area;
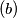
minimal area?
%V0
$(NET 1)$ The vertices of an $(n + 1)-$gon are placed on the edges of a regular $n-$gon so that the perimeter of the $n-$gon is divided into equal parts. How does one choose these $n + 1$ points in order to obtain the $(n + 1)-$gon with
$(a)$ maximal area;
$(b)$ minimal area?